Ülesanne 18 Ülesannete kataloog. Loogilised väited

1. Ülesanne 18 nr 701. Millise nime puhul on väide vale:

(Nime esimene täht on täishäälik→ Nime neljas täht on kaashäälik).

1) ELENA

2) VADIM

3) ANTON

4) FEDOR

Selgitus.

Järeldus on väär siis ja ainult siis, kui eeldus on tõene ja järelikult väär. Meie puhul - kui nime esimene täht on täishäälik ja neljas täht on täishäälik. Nimi Anton vastab sellele tingimusele.

Märge.

Sama tulemus tuleneb järgmistest teisendustest: ¬ (A→ B) = ¬ (¬ A∨ B) = A∧ (¬B).

Õige vastus on loetletud numbril 3.

2. Ülesanne 18 nr 8666. Arvjoonel on kaks lõiku: P = ja Q = . Märkige intervalli A suurim võimalik pikkus, mille jaoks valem

(¬(xA)→ (xP))→ ((xA)→ (xQ))

on identselt tõene, see tähendab, et see võtab muutuja x mis tahes väärtuse jaoks väärtuse 1.

Selgitus.

Teisendame selle väljendi:

(¬ ( xA) → ( x P)) → (( x A) → ( xK))

((xA)∨ (x P))→ ((x Mitte A)∨ (x Q))

¬(( xkuulusA) ∨ ( xkuulusP)) ∨ (( x ei kuulunudA) ∨ ( x kuulusK))

( xei kuulunudA) ∧ ( xei kuulunudP) ∨ ( x kuulusA) ∨ ( x ei kuulunudK)

( xei kuulunudA) ∨ ( x kuulusK)

Seega peab x kuuluma Q-sse või mitte kuuluma A-sse. See tähendab, et kõigi x-ide tõesuse saavutamiseks peab A täielikult Q-s sisalduma. Siis on maksimum, milleks see võib saada, kõik Q, st pikkus 15 .

3. Ülesanne 18 nr 9170. Arvjoonel on kaks lõiku: P = ja Q = .

Märkige lõigu A suurim võimalik pikkus, mille jaoks valem

((xA)→ ¬(xP))→ ((xA)→ (xQ))

identselt tõene, see tähendab, et see võtab muutuja mis tahes väärtuse jaoks väärtuse 1X .

Selgitus.

Teisendame seda väljendit.

(( x€ A) → ¬( xkuulusP)) → (( x kuulusA) → ( x kuulusK))

(( xei kuulunudA) ∨ ( xei kuulunudP)) → (( x ei kuulunudA) ∨ ( x kuulusK))

¬((x ei kuulunud A-sse)∨ (xei kuulunud P-le))∨ ((xei kuulunud A-le)∨ (xkuulus Q-le))

On tõsi, et A∧ B∨ ¬A = ¬A∨ B. Rakendades seda siin, saame:

(x kuulub P-sse)∨ (xei kuulunud A-le)∨ (x kuulub Q-le)

See tähendab, et punkt peab kuuluma Q-le või kuuluma P-le või mitte kuuluma A-le. See tähendab, et A võib katta kõik punktid, mis katavad P ja Q. See tähendab, et A = P Q = = . |A| = 48 - 10 = 38.

4. Ülesanne 18 nr 9202. Hulkade A, P, Q elemendid on naturaalarvud, kus P = (2, 4, 6, 8, 10, 12, 14, 16, 18, 20), Q = (3, 6, 9, 12, 15, 18, 21, 24, 27, 30).

On teada, et väljend

((xA)→ (xP))∨ (¬(xQ)→ ¬(xA))

true (st võtab väärtuse 1) muutuja x mis tahes väärtuse korral.

5. Ülesanne 18 nr 9310. Hulkade A, P, Q elemendid on naturaalarvud, mille P = (2, 4, 6, 8, 10, 12, 14, 16, 18, 20), Q = (5, 10, 15, 20, 25, 30, 35, 40, 45, 50).

On teada, et väljend

((xA)→ (xP))∨ (¬(xQ)→ ¬(xA))

true (st võtab väärtuse 1) muutuja x mis tahes väärtuse korral.

Määrake hulga A suurim võimalik elementide arv.

6. Ülesanne 18 nr 9321. Tähistagem pooltDEL ( n, m ) väide „naturaalarv n jagub naturaalarvuga ilma jäägitam " Mis on suurim naturaalarvA valem

¬ DEL ( x, A ) → (¬ DEL ( x , 21) ∧ ¬ DEL ( x , 35))

on identselt tõene (st võtab muutuja mis tahes loomuliku väärtuse jaoks väärtuse 1x )?

(M.V. Kuznetsova ülesanne)

7. Ülesanne 18 nr 9768. Tähistagem poolt m & n m Ja n 2 & 0101 2 = 0100 2 A valem

x & 29 ≠ 0 → (x & 12 = 0 → x & A ≠ 0)

on identselt tõene (st võtab muutuja mis tahes mittenegatiivse täisarvu jaoks väärtuse 1 X )?

8. Ülesanne 18 nr 9804. Tähistagem poolt m & n mittenegatiivsete täisarvude bitipõhine side m Ja n . Näiteks 14 ja 5 = 1110 2 & 0101 2 = 0100 2 = 4. Mis on väikseim mittenegatiivne täisarv A valem

x & 29 ≠ 0 → (x & 17 = 0 → x & A ≠ 0)

on identselt tõene (st võtab muutuja mis tahes mittenegatiivse täisarvu jaoks väärtuse 1 x )?

9. Ülesanne 18 nr 723. Millise nime puhul kehtib väide:

Kolmanda tähe täishäälik→ ¬ (Esimene täht on kaashäälik \/ Sõnas on 4 vokaali)?

1) Rimma

2) Anatoli

3) Svetlana

4) Dmitri

Selgitus.

Rakendame implikatsiooni teisendust:

Kolmas täht konsonant∨ (Esimene täht Vokaal∧ Sõnal EI ole 4 täishäälikut)

Disjunktsioon on tõene, kui vähemalt üks väide on tõene. Seetõttu sobib ainult 1. variant.

10. Ülesanne 18 nr 4581. Milline antud nimedest vastab loogilisele tingimusele:

(esimene täht on kaashäälik→ viimane täht on kaashäälik) /\ (esimene täht on täishäälik→ kas viimane täht on täishäälik)?

Kui selliseid sõnu on mitu, märkige pikim.

1) ANNA

2) BELLA

3) ANTON

4) BORIS

Selgitus.

Loogiline Ja on tõene ainult siis, kui mõlemad väited on tõesed.(1)

Järeldus on vale ainult siis, kui tõde viitab valele.(2)

Valik 1 sobib kõikidele tingimustele.

Variant 2 ei sobi tingimuse (2) tõttu.

Valik 3 ei sobi tingimuse (2) tõttu.

Variant 4 sobib kõikidele tingimustele.

Pikim sõna tuleb täpsustada, seega on vastus 4.

Ülesanded iseseisvaks lahendamiseks

1. Ülesanne 18 nr 711. Milline antud riiginimedest vastab järgmisele loogilisele tingimusele: ((viimase tähe konsonant) \/ (esimese tähe konsonant))→ (nimi sisaldab tähte "p")?

1) Brasiilia

2) Mehhiko

3) Argentina

4) Kuuba

2. Ülesanne 18 nr 709. Milline antud nimedest vastab loogilisele tingimusele:

(Esimene täht on täishäälik)∧ ((neljanda tähe konsonant)∨ (Sõnal on neli tähte))?

1) Sergei

2) Vadim

3) Anton

4) Ilja

№3

№4

№5. Ülesanne 18 nr 736. Milline antud nimedest vastab loogilisele tingimusele

Esimene täht on täishäälik∧ Neljas täht on kaashäälik∨ Kas sõnas on neli tähte?

1) Sergei

2) Vadim

3) Anton

4) Ilja

Belova T.V.
kuidas õpetada lahendama arvutiteaduse ühtse riigieksami ülesannet 18

valla eelarveline õppeasutus "Lütseum",

Arzamas, jah. bellova. tatjana@ yandex. ru

Enne arvutiteaduse eksamitöö ülesande 18 “Loogilise avaldise õigsuse kontrollimine” lahendamise alustamist tuleb õpilastele selgitada (või meeles pidada), mis on mitme hulga mõiste “liit” ja “ristmik”. Ja kuna ülesanne 18 on seotud segmentide määratlusega, on kõige parem neid mõisteid segmentidel selgitada. Kuid need mõisted on vaja ühendada loogika algebra mõistetega - "konjunktsioon" ja "disjunktsioon" ning loomulikult "inversioon". Toon näite. Kõigepealt vaatame segmendi inversiooni või lihtsamalt öeldes segmendi eitamist.

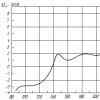
Arvestades lõigu P=. Leidke segmendid, mis on lõigu P= pöördväärtus. Mõelge koordinaatide sirgele (joonis 1):

riis. 1

Sirgele märgime lõigu P (sinine ala), siis on selge, et intervallid, mitte P, on intervallid ja (roheline ala) - joon. 1. Pöörake tähelepanu asjaolule, et lõigu ümberpööramisel ei võeta arvesse punkte 6 ja 15.

Vaatleme teist näidet: on antud kaks segmenti P= ja Q= (antud on samad tähistused, mis ühtse riigieksami ülesandes, et õpilased saaksid märgetega kohe harjuda). Leidke lõik, mis tähistab nende segmentide konjunktsiooni (ühendust) ja disjunktsiooni (ristmikku)

Koordinaatjoonele joonistame segmendid (joonis 2):

riis. 2

Kõigepealt märgime koordinaatjoonele alad, mis tähistavad lõike P (sinine) ja Q (kollane). Seejärel määrame kindlaks, milline koordinaatjoone osa toimib nende kahe segmendi ühendusena. Siinkohal peame meeles, et konjunktsioon on loogiline tehe, mis ühendab kaks lihtsat väidet keeruliseks, kasutades loogilist konnektiivi "ja", ja komplekslause omandab tähenduse "tõene" siis ja ainult siis, kui mõlemad algsed lihtsad väited on tõesed. Seega leiame, et peame leidma piirkonnad, kus eksisteerivad nii segment P kui ka lõik Q ning selliseid piirkondi on ainult üks – segment (punane). Uurime üksikasjalikumalt kõiki sirgeid segmente, et õpilased saaksid materjalist selgemalt aru saada, nii et:

Vaatame nüüd nende segmentide disjunktsiooni sarnaselt. Pöördume uuesti selle loogilise tehte definitsiooni juurde - "disjunktsioon on loogiline tehe, mis vastavalt kahele või enamale loogilisele lausele paneb uue, mis on tõene siis ja ainult siis, kui vähemalt üks sisendi alglausetest on tõsi." See tähendab, et me peame leidma koordinaatjoonelt intervallid, kus on vähemalt üks meie algsetest lõikudest, see soovitud intervall on roheline (joonis 2). Samuti analüüsime iga intervalli ja näitame, et see on tõesti nii:

Leitud intervalle kombineerides saame, et vajalik segment, mis tähistab algsete segmentide disjunktsiooni, on segment – ​​roheline (joonis 2).

Pärast selle näite analüüsimist võite lasta õpilastel proovida leida erinevaid loogikatehte kombinatsioone – disjunktsiooni, konjunktsiooni ja eitust. Näiteks antud kaks segmenti P=[-4,10] ja Q=. Leidke segment, mis tähistab järgmisi loogilisi tehteid: , , (nende loogiliste operatsioonide kombinatsioonid on erinevad).

riis. 3

riis. 4

riis. 5

Kui kõik näited on analüüsitud, ei teki õpilastel raskusi arvutiteaduse ühtse riigieksami eksamitöö ülesande nr 18 mõistmisel ja lahendamisel.

Siin on näiteid mitme ülesande lahendustest:

Arvjoonel on kaks segmenti: P = ja Q =. Valige segment A nii, et valem

(x  A) → ((x  P) → (x  K)) on identselt tõene, see tähendab, et see võtab muutuja mis tahes väärtuse jaoks väärtuse 1 X. Võimalikud vastused:

1) 2) 3) 4)

Lahendus (joonis 6): avaldise mõistmise lihtsustamiseks tähistame üksikuid väiteid tähtedega - A: x A,P: x P,K: x K. Seega saame asendust arvesse võttes järgmise avaldise: → ( P→ )=1. Avaldise 1 võrdsus tähendab, et olenemata muutuja väärtusest X me ei võtnud seda, meie loogiline avaldis võtab väärtuse 1, see tähendab kogu arvureal. Tuletame meelde mõned loogilised seadused ja võrdsused ning teisendame oma avaldist: =1. Selle tulemusena leiame, et peame konstrueerima disjunktsiooni kolmest segmendist, millest kaks on meile teada. Ehitame need (joon. 7). Alustuseks, nagu kõigis ülaltoodud näidetes, peame konstrueerima segmentide P (oranž) ja Q (punane) inversioonid. Seejärel saame kogu avaldisest määrata disjunktsiooniintervallid =1 (rohelised alad joonisel 7). Seega leiame, et meil on "vaba" osa koordinaatjoonel - . See osa on sirge ja peaks soovitud segmendiga kattuma A.

On teada, et väljend

((x ∈ A) → (x ∈ P)) ∧ ((x ∈ Q) → ¬(x ∈ A))

tõene (st võtab väärtuse 1) muutuja x mis tahes väärtuse korral. Määrake hulga A suurim võimalik elementide arv.

Lahendus.

Tutvustame järgmist tähistust:

(x ∈ P) ≡ P; (x ∈ Q) ≡ Q; (x ∈ A) ≡ A; ∧ ≡ · ; ∨ ≡ +.

Seejärel, rakendades implikatsiooniteisendust, saame:

(¬A + P) · (¬Q + ¬A) ⇔ ¬A · ¬Q + ¬Q · P + ¬A + ¬A · P ⇔

⇔ ¬A · (¬Q + P + 1) + ¬Q · P ⇔ ¬A + ¬Q · P.

Nõutakse, et ¬A + ¬Q · P = 1. Avaldis ¬Q · P on tõene, kui x ∈ (2, 4, 8, 10, 14, 16, 20). Siis peab ¬A olema tõene, kui x ∈ (1, 3, 5, 6, 7, 9, 11, 12, 13, 15, 17, 18, 19, 21, 22, 23,...).

Seetõttu on hulga A maksimaalne elementide arv, kui A sisaldab kõiki hulga ¬Q · P elemente, selliseid elemente on seitse.

Vastus: 7.

Vastus: 7

Hulga A elemendid on naturaalarvud. On teada, et väljend

(x (2, 4, 6, 8, 10, 12)) → (((x (3, 6, 9, 12, 15)) ∧ ¬(x A)) → ¬(x (2, 4, 6) , 8, 10, 12)))

Lahendus.

Tutvustame järgmist tähistust:

(x ∈ (2, 4, 6, 8, 10, 12)) ≡ P; (x ∈ (3, 6, 9, 12, 15)) ≡ Q; (x ∈ A) ≡ A.

Muutmisel saame:

P → ((Q ∧ ¬A) → ¬P) = P → (¬(Q ∧ ¬A) ∨ ¬P) = ¬P ∨ (¬(Q ∧ ¬A) ∨ ¬P) = ¬P ∨ ¬Q ∨ A.

Loogiline VÕI on tõene, kui vähemalt üks väide on tõene. Avaldis ¬P ∨ ¬Q kehtib kõigi x väärtuste kohta, välja arvatud väärtused 6 ja 12. Seetõttu peab intervall A sisaldama punkte 6 ja 12. See tähendab, et minimaalne punktide kogum intervallis A ≡ ( 6, 12). Hulga A elementide summa on 18.

Vastus: 18.

Vastus: 18

Hulkade A, P, Q elemendid on naturaalarvud, kus P = (2, 4, 6, 8, 10, 12, 14, 16, 18, 20), Q = (3, 6, 9, 12, 15, 18, 21, 24, 27, 30).

On teada, et väljend

true (st võtab väärtuse 1) muutuja x mis tahes väärtuse korral. Määrake hulga A elementide summa väikseim võimalik väärtus.

Lahendus.

Lihtsustame:

¬(x P) ∨ ¬(x Q) annab 0 ainult siis, kui arv asub mõlemas hulgas. See tähendab, et selleks, et kogu avaldis oleks tõene, peame panema kõik P-s ja Q-s olevad arvud A-sse. Sellised arvud on 6, 12, 18. Nende summa on 36.

Vastus: 36.

Vastus: 36

Allikas: Arvutiteaduse õppetöö, 11. hinne 18. jaanuar 2017 Valik IN10304

Hulkade A, P, Q elemendid on naturaalarvud, kus P = (2, 4, 6, 8, 10, 12, 14, 16, 18, 20), Q = (3, 6, 9, 12, 15, 18, 21, 24, 27, 30).

On teada, et avaldis ((x A) → (x P)) ∨ (¬(x Q) → ¬(x A))

true (st võtab väärtuse 1) muutuja x mis tahes väärtuse korral.

Määrake hulga A suurim võimalik elementide arv.

Lahendus.

Teisendame selle väljendi:

((x A) → (x P)) ∨ ((x Q) → (x A))

((x A) ∨ (x P)) ∨ ((x Q) ∨ (x A))

(x A) ∨ (x P) ∨ (x Q)

Seega peab element kas sisalduma P-s või Q-s või mitte sisalduma A-s. Seega saab A sisaldada ainult elemente P-st ja Q-st. Kokku on neis kahes hulgas 17 mittekorduvat elementi.

Vastus: 17

Hulkade A, P, Q elemendid on naturaalarvud ja P = (1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21), Q = (3, 6, 9, 12, 15, 18, 21, 24, 27, 30). On teada, et väljend

((x P) → (x A)) ∨ (¬(x A) → ¬(x Q))

true (st võtab väärtuse 1) muutuja x mis tahes väärtuse korral. Määrake hulga A elementide summa väikseim võimalik väärtus.

Lahendus.

Avaldame kaks tähendust. Saame:

(¬(x P) ∨ (x A)) ∨ ((x A) ∨ ¬(x Q))

Lihtsustame:

(¬(x P) ∨ (x A) ∨ ¬(x Q))

¬(x P) ∨ ¬(x Q) annab 0 ainult siis, kui arv asub mõlemas hulgas. See tähendab, et selleks, et kogu avaldis oleks tõene, peate sisestama kõik P ja Q numbrid A-sse. Need arvud on 3, 9, 15 ja 21. Nende summa on 48.

Vastus: 48.

Vastus: 48

Allikas: Arvutiteaduse õppetöö, 11. hinne 18. jaanuar 2017 Valik IN10303

Ja väljend

(y + 2x 30) ∨ (y > 20)

X ja y?

Lahendus.

Pange tähele, et selleks, et see avaldis oleks identselt tõene, tuleb avaldis (y + 2x Vastus: 81.

Vastus: 81

Allikas: Ühtne riigieksam - 2018. Varajane laine. Valik 1., Ühtne riigieksam - 2018. Varajane laine. 2. võimalus.

Arvjoonele on antud segment A. On teada, et valem

((x ∈ A) → (x 2 ≤ 100)) ∧ ((x 2 ≤ 64) → (x ∈ A))

kehtib identselt iga reaalse kohta x. Mis on lõigu A lühim pikkus?

Lahendus.

Laiendades implikatsiooni vastavalt reeglile A → B = ¬A + B, asendades loogilise summa hulgaga ja loogilise korrutise seostesüsteemiga, määrame parameetri väärtused A, mille juures agregaatide süsteem

on lahendused mis tahes reaalarvude jaoks.

Et süsteemi lahendid oleksid kõik reaalarvud, on vajalik ja piisav, et iga kogumi lahendid oleksid kõik reaalarvud.

Võrratuse lahendid on kõik arvud vahemikust [−10; 10]. Et kogu kehtiks kõigi reaalarvude jaoks, siis arvud x, mis ei asu määratud lõigul, peab kuuluma lõigu A. Järelikult ei tohi lõik A minna kaugemale lõigu piiridest [−10; 10].

Samamoodi on ebavõrdsuse lahendused kiirte arvud ja selleks, et kogum kehtiks kõigi reaalarvude jaoks, on arvud x, mis ei asu näidatud kiirtel, peab asuma segmendil A. Järelikult peab lõik A sisaldama lõiku [−8; 8].

Seega võib segmendi A lühim pikkus olla 8 + 8 = 16.

Vastus: 16.

Vastus: 16

A väljendus

(y + 2x ≠ 48) ∨ (A x) ∨ ( x y)

on identselt tõene, st võtab mis tahes mittenegatiivsete täisarvude jaoks väärtuse 1 x Ja y?

Lahendus.

A x Ja y, mõelgem, millistel juhtudel on tingimused ( y + 2x≠ 48) ja ( x y) on valed.

y = 48 − 2x) ja (x ≥ y). See x vahemikus 16 kuni 24 ja y vahemikus 0 kuni 16. Pange tähele, et selleks, et avaldis sobiks mis tahes x Ja y, tuleb võtta x= 16 ja y= 16. Siis A A on võrdne 15-ga.

Vastus: 15.

Vastus: 15

Allikas: arvutiteaduse ühtne riigieksam 28.05.2018. Pealaine, A. Imajevi versioon - “Kotolis”.

Mis on suurim mittenegatiivne täisarv A väljendus

(y + 2x ≠ 48) ∨ (A x) ∨ ( A y)

on identselt tõene, st võtab mis tahes mittenegatiivsete täisarvude jaoks väärtuse 1 x Ja y?

Lahendus.

Suurima mittenegatiivse täisarvu leidmiseks A, mille juures väljend on x Ja y, mõelgem, millistel juhtudel on tingimus ( y + 2x≠ 48) on vale.

Seega leiame kõik lahendused, kui ( y = 48 − 2x). See x vahemikus 0 kuni 24 ja y vahemikus 48 kuni 0. Pange tähele, et selleks, et avaldis sobiks mis tahes x Ja y, tuleb võtta x= 16 ja y= 16. Siis A A on võrdne 15-ga.

Vastus: 15.

Vastus: 15

Allikas: 2019. aasta arvutiteaduse ühtse riigieksami demoversioon.

Mis on väikseim mittenegatiivne täisarv A väljendus

(2x + 3y > 30) ∨ (x + y ≤ A)

kehtib identselt kõigi mittenegatiivsete täisarvude puhul x Ja y?

Lahendus.

A, milles avaldis on identne kõigi mittenegatiivsete täisarvude puhul x Ja yy + 2x> 30) on vale.

y + 2x≤ 30). See x vahemikus 0 kuni 15 ja y vahemikus 10 kuni 0. Pange tähele, et selleks, et avaldis sobiks mis tahes x Ja y, tuleb võtta x= 15 ja y= 0. Siis 15 + 0 ≤ A. Seega väikseim mittenegatiivne täisarv A on võrdne 15-ga.

Vastus: 15.

Vastus: 15

Mis on suurim mittenegatiivne täisarv A väljendus

(2x + 3y x+ y ≥ A)

kehtib identselt kõigi mittenegatiivsete täisarvude puhul x Ja y?

Lahendus.

Suurima mittenegatiivse täisarvu leidmiseks A, milles avaldis on identne kõigi mittenegatiivsete täisarvude puhul x Ja y, mõelgem, millistel juhtudel on tingimus (3 y + 2x Seega leiame kõik lahendused, kui (3 y + 2x≥ 30). See x rohkem kui 15 ja y suurem kui 10. Pange tähele, et selleks, et avaldis sobiks mis tahes x Ja y, tuleb võtta x= 0 ja y= 10. Siis 0 + 10 ≤ A. Seega suurim mittenegatiivne täisarv A võrdub 10-ga.

Vastus: 10.

Vastus: 10

Mis on väikseim mittenegatiivne täisarv A väljendus

(3x + 4y ≠ 70) ∨ (A > x) ∨ (A > y)

kehtib identselt kõigi mittenegatiivsete täisarvude puhul x Ja y?

Lahendus.

Väikseima mittenegatiivse täisarvu leidmiseks A, milles avaldis on identne kõigi mittenegatiivsete täisarvude puhul x Ja y, mõelgem, millistel juhtudel on tingimus (3 x + 4y≠ 70) on vale.

Seega leiame kõik lahendused, kui (3 x + 4y= 70). See x vahemikus 2 kuni 22 ja y vahemikus 16 kuni 1. Pange tähele, et selleks, et avaldis sobiks mis tahes x Ja y, tuleb võtta x= 10 ja y= 10. Siis A> 10. Seega väikseim mittenegatiivne täisarv A võrdub 11.

1. Näide demoversioonist

(esimese tähe konsonant → teise tähe kaashäälik) / (eelviimane tähtvokaal → viimase tähe vokaal)

1) KRISTINA 2) MAXIM 3) STEPAN 4) MARIA

Lahenduse eskiis Implikatsioon a → b on samaväärne avaldisega ¬a / b.

Esimene vihje kehtib sõnade KRISTINA ja STEPAN kohta. Nendest sõnadest kehtib teine ​​​​tähendus ainult sõna KRISTINE kohta.

Vastus: 1. KRISTINA

2. Veel kaks näidet

Näide 1 (FIPI panga avatud segment)

Milline antud nimedest vastab loogilisele tingimusele:

(esimene kaashäälik → esimene vokaal) / (viimane vokaal → viimane kaashäälik)

1. IRINA 2. MAXIM 3. ARTEM 4. MARIA

Lahenduse eskiis. Implikatsioon a → b on samaväärne avaldisega ¬a / b. See avaldis on tõene, kui kumbki avaldis a on väär või mõlemad avaldised a ja b on tõesed. Kuna meie puhul ei saa üheski implikatsioonis olla tõesed mõlemad avaldised korraga, peavad väited “esimene täht on kaashäälik” ja “viimane täht on täishäälik” olema väärad, see tähendab, et vajame sõna, mis esimene täht on täishäälik ja viimane on kaashäälik.

Vastus: 3. ARTEM.

Näide 2. Millise arvu X näidatud väärtuste puhul on väide tõene?

(X< 4)→(X >15)

1) 1 2) 2 3) 3 4) 4

Lahendus. Ükski arv ei saa olla väiksem kui 4 ega suurem kui 15. Seetõttu on implikatsioon tõene ainult siis, kui eeldus X< 4 vale.

Vastus 4.

2. Ülesanded ühtse riigieksami 2013-2014 vormingus.

2.1. Demoversioon 2013

Arvjoonel on kaks lõiku: P = ja Q = .

Valige segment A nii, et valem

1) 2) 3) 4)

2.2. Demoversioon 2014

Arvjoonel on kaks lõiku: P = ja Q = . Pakutud segmentide hulgast valige segment A, mis vastab loogilisele avaldisele

((x ∈ P) → ¬ (x ∈ Q)) → ¬ (x ∈ A)

identselt tõene, see tähendab, et see võtab muutuja mis tahes väärtuse jaoks väärtuse 1

Vastusevariandid: 1) 2) 3) 4)

Lahendus. Teisendame avaldise kasutades . Meil on:

¬((x ∈ P) → ¬ (x ∈ Q)) ∨ (¬ (x ∈ A)) - implikatsiooni asendamine disjunktsiooniga;

¬(¬(x ∈ P) ∨ ¬ (x ∈ Q)) ∨ (¬ (x ∈ A)) - implikatsiooni asendamine disjunktsiooniga;

((x ∈ P) ∧ (x ∈ Q)) ∨ (¬ (x ∈ A)) - de Morgani reegel ja topelteituse eemaldamine;

(x ∈ A) → ((x ∈ P) ∧ (x ∈ Q)) - disjunktsiooni asendamine implikatsiooniga

Viimane avaldis on identselt tõene siis ja ainult siis, kui A ⊆ P∩ Q = ∩ = (vt ). Neljast etteantud segmendist vastab sellele tingimusele ainult segment – ​​valik nr 2.

Vastus: - variant nr 2

3. Ülesanded ühtse riigieksami 2015-2016 vormingus.

3.1. Ülesanne 1.

Arvjoonel on kaks lõiku: P = ja Q = .

On teada, et lõigu A piirid on täisarvulised punktid ja lõigu A jaoks valem

((x ∈ A) → (x ∈ P)) \/ (x ∈ Q)

on identselt tõene, see tähendab, et see võtab muutuja x mis tahes väärtuse jaoks väärtuse 1.

Mis on lõigu A suurim võimalik pikkus?

Õige vastus : 10

Lahendus:

Teisendame avaldise – asendame implikatsiooni disjunktsiooniga. Saame:

(¬(x ∈ A)) \/ ((x ∈ P)) \/ (x ∈ Q)

Avaldis ((x ∈ P)) \/ (x ∈ Q) kehtib ainult nende x kohta, mis asuvad kas P-s või Q-s, teisisõnu, kui x ∈ R = P ∪ Q = ∪ . Väljendus

(¬(x ∈ A)) \/ (x ∈ R)

on identselt tõene siis ja ainult siis, kui A ∈ R. Kuna A on lõik, siis A ∈ R siis ja ainult siis, kui A ∈ P või A ∈ Q. Kuna lõik Q on pikem kui lõik P, siis on lõigu suurim pikkus segment A saavutatakse, kui A = Q = . Lõigu A pikkus on sel juhul 30–20 = 10.

3.2. 2. ülesanne.

Tähistagem poolt m&n mittenegatiivsete täisarvude bitipõhine side m Ja n. Näiteks 14&5 = 1110 2 &0101 2 = 0100 2 = 4. Mis on väikseim mittenegatiivne täisarv A valem

x&25 ≠ 0 → (x&33 ≠ 0 → x&A ≠ 0)

on identselt tõsi, st. võtab muutuja mis tahes mittenegatiivse täisarvu väärtuseks 1 X?

Õige vastus : 57

Lahendus:

Teisendame avaldise – asendame implikatsioonid disjunktsioonidega. Saame:

¬( x&25 ≠ 0) ∨ (¬( x&33 ≠ 0) ∨ x&A ≠ 0)

Avame sulud ja asendame ebavõrdsuse eitused võrdustega:

x&25 = 0 ∨ x&33 = 0 ∨ x&A ≠ 0 (*)

Meil on: 25 = 11001 2 ja 33 = 100001 2. Seetõttu valem

x&25 = 0 ∨ x&33 = 0

väär siis ja ainult siis, kui arvu kahendesitus x sisaldab 1-t vähemalt ühes järgmistest kahendnumbritest: 100000 (32), 10000 (16), 1000 (8) ja 1.

Et valem (*) oleks tõene kõigi selliste kohta x On vajalik ja piisav, et arvu A binaarne esitus sisaldab kõigis nendes bitides 1. Väikseim selline arv on arv 32+16+8+1 = 57.